The 3×3 magic square is commonly referred to as Ghazali’s magic square, because it is listed in the book Deliverance From Error (al-munqidh min al-ḍalāl) created by Imam Al-Ghazali. However, it should be noted that the origin of the 3×3 magic square was first used by Chinese Mathematicians in 650 BC during the Ching Dynasty from the legendary “Luoshu (洛書) or “The Letter Scroll of the Lo River“, and openly since 570 AD. And appeared to Islamic Mathematicians in the 7th century AD. According to Chinese legend, since the great flood, King Yu was trying to drain the water to be discharged into the sea, then a turtle appeared with a strange shell pattern. 3×3 columns with vertical and horizontal row columns and diagonal numbers totaling 15. According to legend afterwards people used this pattern to control rivers and protect against floods.
In 983 AD, the magic square with 5×5 and 6×6 patterns emerged from Arabic mathematics in Baghdad. Since the first literature done by Jabin Ibn Hayyan (721-815) and Al-Ghazali (1058-1111) AD, then it was preserved in the tradition of planetary tables.
3×3 magic square is a magic square that has 9 squares with 3 columns and 3 rows. 3×3 magic square has a standard form (Tabi’i) as shown above Each 3×3 magic square has the AS number 12. The number 12 is obtained from 3×3 = 9. Then 9 minus 1 = 8. The number 8 times 1.5 = 12.
The number 1.5 is obtained from 3 divided by 2 = 1.5. from this calculation, we get the AS 12.
Miftah is the opening number, the magic square Tabi’i has a Miftah of 1.
Each column of the 3×3 magic square has a constant value of 15, ie:
4+9+2=15 | 3+5+7=15 | 8+1+6=15
4+3+8=15 | 9+5+1=15 | 2+7+2=15
How to Enter Numbers (n) In 3×3 Magic Square ?
How to make a 3×3 magic square from the number 66?
Answer:
You know (n) is 66 and the AS of 3×3 magic square is 12 then find the miftah first
= (66-12) : 3
= 54: 3
=18
The result 18 is the miftah number, we enter it into column number 1 by changing number 1 to 18. Then we enter the number in column 2 by miftah + 1, which is 19 by changing number 2 to 19. Then we enter the number in column 3 by miftah + 2, which is 20. And so on, the results are like the table below:
| 4 | 9 | 2 | 4 | 9 | 2 | 21 | 26 | 19 | ||
| 3 | 5 | 7 | ▶ | 3 | 5 | 7 | ▶ | 20 | 22 | 24 |
| 8 | 1 | 6 | 8 | 18 | 6 | 25 | 18 | 23 |
Using Kalkulator Hisab, just input the numbers as shown below and get 3×3 magic square for (4) four elements:
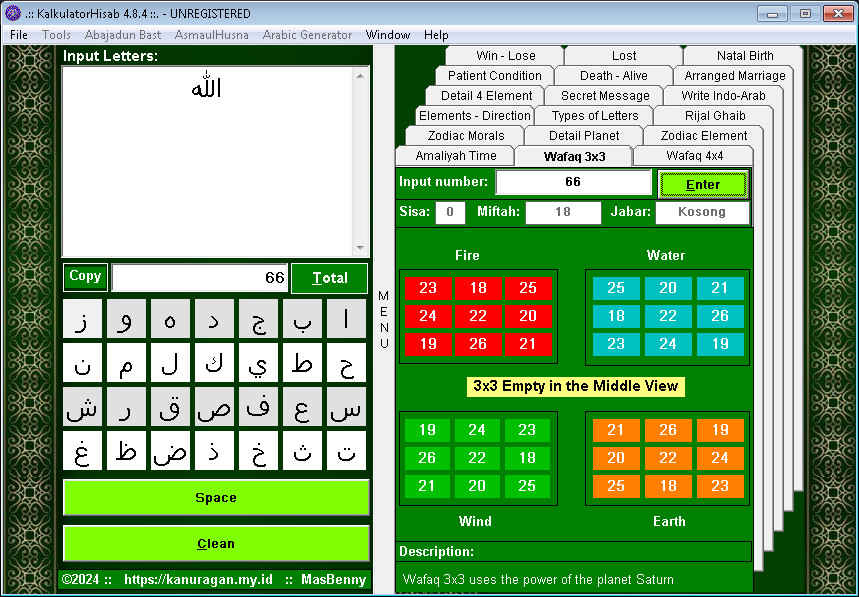
So if we use Kalkulator Hisab, we don’t need to bother and spend a lot of time calculating like this, right?








Leave a Comment